Osakeste liikumisest

Liikumise kirjeldamiseks on tavaliselt positsioonivektor r, mis arvestab ka ajaga (t). Ülakirjelduse järgi on O alguspunkt ja P selle uus asukoht.

Seda saab täpsemalt väljendada mitut moodi. Esimeses reas on lihtsalt 3 koordinaattelje suhtes väljendatud muutused. Katusega e tähed on väärtusega 1 ühik selles teljel või trajektooril ning x, y või z võib näidata mitme e kordselt see liigub ühe ajaühiku kohta.

Teine ja kolmas r rida kirjeldasid vastavalt liikumist keral ja silindril ning ka nendel kõveratel pindadel on e pikkus väärtusega 1.

Magnetvälja mõju (kalkulaator) languga osakestele.

Kui laenguga osake läbib magnetvälja trajektooriga, mis ei ole paralleelne magnetvälja jõujoontega, siis hakkab osake ümber selle jõujoone tiirlema.

Sellisel juhul osakestele mõjuv (tiirlema sundiv) jõud newton'ites leitav ülal oleva valemiga, kus võetakse siinus nrugast, mis jääb jõujoone suuna ja osakese suuna vahele. Osakese kiirus on v (meetrites sekundis), magnetvälja intentsiivsus teslades B ja osakese laeng q kulonites.
Lihtsustatud näitena kui 1 kulon läbib 90 kraadiselt ristuvalt 1 teslase magnetvälja 1 meeter sekundis, siis mõjub sellele  1 newton.

Osakesele mõjuv kiirendus (a) on leitav seosena kiirendus= sellele mõjuv jõud newton'ites jagatud osakese või objekti massiga.

Lihtsustatud olukord objektide kokkupõrkest, kui mõlemad objektid saavad ainult ühisel sirgjoonel liikuda ning kokkupõrgetel säilib energia. Kiirused enne kokkupõrget on u1 ja u2 ning kiirused pärast kokkupõrget on v1 ja v2. Number näitab vastavalt kumma massiga objekti see kirjeldab.

Lihtsustatud surve jõu valemid kui osakesed põrkavad kahe seina vahel. Ülakriips tähendab keskmist. Seinte vaheline distants on L ja molekulide arv N. Keskmine jõud on sellises olukorras (molekulide arv x nende mass x kiirus ruudus)/seinte vaheline distants. Võimalik, et kuubi kujulises ruumis võib kogu surve jõud olla umbkaudu 3 korda suurem kui kõigi seinte vahel käib ühtlane põrkumine.  

Molekulide kiiruste valemid ideaalse gaasi võrrandi järgi.Vp on kõige tõenäolisem kiirus ja v ülakriipsuga keskmine. Absoluutne temperatuur on T, osakeste arv moolides M ja R on universaalne gaasikonstant. Teades 3 väärtuse suurust saab leida keskkonnas olevate osakeste tõenäolisemad kiirused. 

Olukord kus objektid massiga m1 ja m2 liiguvad peaaegu otse üksteise suunas kiirustega v1 ja v2 kuid põrkuvad punktis A veidi nurga all, mis põhjustab põrkumist nurkade all teeta 1 ja teeta 2 kiirustega v1f ja v2f.

m 1 v 1o - m 2 v 2o

=

m 1 v 1fcosθ 1 + m 2 v 2fcosθ 2

Valem x teljel ühes suunas olevast kineetilisest energiast (y telge siin ei arvestata kuid valemis). Kuna m2 liigub -x suunas, siis siin olukorras oli selle väärtus +x suuna jaoks negatiivne. Paremal pool võrdusmärki on x suunaline liikumine samuti arvesse võetud. Koosinus on x teljest 0 kraadise kõrvalekalde puhul väärtusega 1 ning 90 kraadise kõrvalekalde korral 0 ehk x suunaline liikumine puuduks.  

0

=

m 1 v 1fsinθ 1 + m 2 v 2fsinθ 2

Y teljel toimuva kõrvalekalde valem. Enne kokkupõrget oli see 0 ja seetõttu oli valemis vasakul pool võrdusmärki 0. Parempoolne osa kirjeldab samuti kokkupõrke järgset liikumist. Siinus 0 on 0 (y väärtus ei muutu) ja siinus 90 kraadist on 1 (y väärtus muutub maksimaalselt).

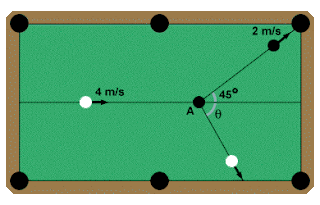
Veidi sarnane olukord piljardipallidega. Must pall oli algselt paigal kuid liigub pärast kokkupõrget valge palli algsest trajektoorist 45 kraadi all edasi. Mõlemad pallid on 0,5 kg ning kiirused ühtlustuvad pärast kokkupõrget. Ka siin tuleb liikumine x ja y telje suhtes eraldi leida.

.5(4)	=	.5v 1cosθ + .5(2)cos 45
4	=	v 1cosθ +

Valge palli liikumine x telje suhtes.

0	=	2 sin 45 - v 1sinθ
	=	v 1sinθ
v 1	=

Y telje suhtes toimuv liikumine.

4	=	()cosθ +
4 -	=	(cotθ)
cotθ	=	1.83
θ	=	28.7 o

X telje suhtes toimuv valge palli kõrvalekaldeks vajalik arvutuskäik teades liikumist x ja y telje suhtes.

Gaasilise osakeste keskmine kineetiline energia (KEavg) on ühe molekuli kohta leitav seosega3/2(kT).
See kineetiline energia näitab ka osakese kiirust ning osakeste kineetiline energia võrdub ka massi ja kiiruse ruudu korrutisega.

Osakese kiirusest sõltub kui kaugele see jõuab liikuda kokkupõrgete vahel. Ülemise valemi puhul arvestati silindri kujulise ruumiga kuid umbkaudselt peaks see kehtima ka teiste ruumi kujude puhul. Lihtsustatult: vaba liikumise distants = osakeste liikumiskiirus/(ruumi ruumala x osakeste hulk ruumala ühikus).