Alternatiivsetest numbrisüsteemidest

Erinevate numbrisüsteemide sarnane omadus on võimalus arvu jagada või korrutada numbrisüsteemi eri sümbolite arvuga. Selleks tehteks peab arvu lõpust vastavalt võtma nulli või lisama nulli. Kümnendsüsteemis tähendab 0 lisamine täisarvu lõppu 10'ga korrutamist ja lõpus oleva nulli eemaldamisega saab kümnega jagada.
Arvutite kahendsüsteemis saab nullide eemalduse ja lisamisega arvu jagada või korrutada kahega.

All on näited kahendsüsteemi numbritest kümneni. Kasutatakse saadaolevaid sümboleid ja järjest lugemisel moodustatakse arvudest järgmine minimaalselt suurem number.
0=0
1=1
2=10
3=11
4=100
5=101
6=110
7=111
8=1000
9=1001
10=1010

Näiteks kui kahte (10) jagada kahega, siis saab 1. Kui lisada 0 saab 100 (4). Selliste tehetega ei pea teadma mis numbritega on tegu ning neid tehteid saab teha keegi kes ei oskaks neid numbreid lugeda või üldse mõni masin.

Kolme sümboliga numbrisüsteemis kordub sarnane omadus kuid selles saab kergesti jagada ja korrutada kolmega.

0=0
1=1
2=2
3=10
4=11
5=12
6=20
7=21
8=22
9=100
10=101

9/3=100/10=3 ehk 10.

11 sümboliga numbrisüsteem. Lisanumber on X.

0=0
1=1
2=2
3=3
4=4
5=5
6=6
7=7
8=8
9=9
10=X
11=10
12=11
13=12
14=13
15=14
16=15
17=16
18=17
19=18
20=19
21=1X
22=20

Sellise süsteemiga saab kergesti 11'ga jagada.

Arvutite jaoks saab eri numbri tähistuste kasutamisel lihtsustada kindlate arvudega jagamist. Täpsus kannatab kui arvu lõpus oli 0 asemel midagi muud kuid see vea suurus väheneb suuremate arvudega. 

Maatriksite kasutusalasid

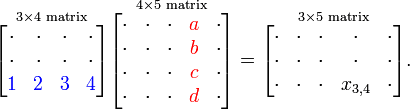
Matemaatilisi maatrikseid saab kasutada lihtsustatult objekti liikumise või muutmise kirjeldamiseks kuigi maatriksite omavaheline korrrutamine on harjumist nõudva loogikaga. Üldiselt peab mingi koha väärtuse leidmiseks korrutama väärtused, mis ristusid selles kohas ning saadud väärtused liidetakse kokku.

Lihtsamas olukorras kui maatriks korrutatakse lihtsalt ühe väärtusega, siis korrutatakse iga selles olev väärtus selle numbriga läbi.

Näide maatriksi mõõtmete muutusest nende omavahel korrutamisel ning ühe näitelise suuruse leidmisest.

Üks maatriksite korrutamise kasutusala on äris käibe kirjeldamises.

 Näiteks maatriks A read võivad tähistada erinevaid kliente ja tulbad neile müüdud erinevate toodete hulka.

Maatriks B iga rida käib ühe eraldi toote kohta. Esimene tulp kirjeldab hinda ja teine tulp toote kaalu.

Et leida kui palju kulutas esimene firma toodete ostmisele, tuleb selle firma rea info korrutada toodete hinna tulbaga.

Esimesele firmale müüdud toodete massi leidmiseks võetakse selle firma andmed ja korrutatakse need kaalude tulbaga.

Korrates seda iga firmaga saab kokkuvõtva tabeli sellel aastal iga firma poolt ostetust raha ja kaalu järgi.

Graafikas kasutatakse maatrikseid punktide uute asukohtade arvutamiseks. Siinsed näited on lihtsamad ja ainult ühe teljega arvestavad kuid kui näiteks pöörlemine või peegeldumine ei käi ainult ühe telje ümber, siis on valemid tavaliselt kordades pikemad.
Tavaliselt on esimene rida ja tulp x telje väärtuste jaoks, teine rida/tulp y jaoks ning kolmas rida ja tulp z telje väärtuste jaoks.
Pildi pööramises ümber punkti.

Ülakomaga leitavad väärtused näitavad, mis on uued x ja y väärtused. Lahutamistehe x' reas kehtib ainult vastupäeva pöörlemisel. Maatriksi sees olevad tehted on üldiselt samasugused kui maatriksit mittekasutavad x ja y väärtuse leidmise valemid. Näiteks kui pöörlemine käib ümber teljestiku nullpunkti, punkt asus algselt kohas x=1 y=0 ning kui pöörati 90 kraadi (sin90=1 ja cos90=0) vastupäeva, siis saab punkti uueks asukohaks x=0 y=1.

Esimene maatriks kirjeldab kellaosuti suunas pöörlemist ja teine vastupäeva pöörlemist.

Peegeldumises x teljelt jäetakse x väärtused samaks kuid y väärtused korrutatakse läbi -1'ga, mis viiks punkti sama kaugele teisele poole x telge.

Peegeldumine ümber y telje.

Suurendamises (ülanäites kahekordselt) igas suunas korrutatakse x ja y väärtused kindla arvuga läbi.

Näide (m=1,25) horisontaalsest nihkest. Musta täpiga on näha horisontaal mille suhtes nihkutakse. Mida kaugemal sellest asub mingi horisontaal seda rohkem on see nihkes.

 

Esimene tehe on horisontaalse nihke oma ja teine vertikaalse nihke oma.

 Projektsiooniga leitakse väärtused ühel teljel. 

Ülamaatriks kehtib projektsioonis y teljele. Selle järgi jäetakse y väärtused endiseks ning x väärtused korrutatakse nulliga.

Surumine kui ei saa tihedamaks kokku suruda ja ühes suunas surumisele peab kaasnema teises suunas kasvamine. Näiteks kui kõrgust y vähendada 2 korda (1/2), siis peaks laius x kasvama 2 korda.

Mitme muutujaga integraalid

Mitme muutujaga integraalides on üle 1 muutuja nagu näiteks f(x,y) või f(x,y,z) ning sellisel juhul on tavaliselt mitu integraalisümbolit tehte alguses reas ning füüsikavalemites võib tihti mitut integraalisümbolit reas näha. Kahe muutujaga funktsioonid nagu näiteks z=f(x,y) võivad kirjeldada ruumala kuigi ruumala saab ka kolme muutujaga kirjeldada. 

Kui ühe muutujaga integraal kirjeldas mingi piirkonna pindala, siis alates kahe muutujaga funktsioonist kirjeldaks see ruumala. Sama ruumala saas kirjeldada kolme muutujaga funktsioonis f(x, y, z)=1.
Kui on risttahukas küljepikkustega 4x5x6 ja funktsiooniga f(x, y)=5 siis saab seda tähistada stiilis:

 D on selle kujundi aluseks tasapinnal xy.

Kui selle kujundi alus on mõõtudega 3 ≤ x ≤ 7, 4 ≤ y ≤ 10, siis kehtib ülemine valem. Korraga integreeritakse x või y suhtes leides mõlemaga F(b)-F(a) väärtuse. Lahendamine käib tavaliselt parempoolsest integraalimärgist vasakpoole integraalimärgi suunas.

Kui leida integraal x jaoks, siis oleks saaks 5 dx asemel 5x+C ja F(b)-F(a) tähendaks (5x7+C)-(5x3+C). Mitme integraalimärgi korral lahendatakse neid tavaliselt paremalt vasakule võttes vastava integraalimärgi küljest algus- ja lõppkoordinaadi.

Ala D ruumala üks võimalik esitusviis.

Kuubi ruumala valem kui kogu kujund on valemiga f(x,y,z)=1. Järjest leitakse väärtused x, y ja z jaoks F(b)-F(a) tehetega kuni saadakse ruumala 1. Näiteks F(1)-F(0) on siinkohas väärtusega 1-0.

Kui funktsioon f kirjeldab tihedust punktis (x, y, z) seosega f=x+y+z, siis saab ruumala integreerimisega leida kujundi massi.

Korraga leitakse x või y või z väärtus ja saadud arvulised väärtused liidetakse omavahel. Ülemise integreerimisseosega kasvab integreerimisel muutuja aste ühe võrra ning arv jagatakse läbi astmega, mis annaks x asemel x ruudus jagatud 2 kuid kui x väärtus on 1, siis on selle koguväärtus 1/2, mis jäi pärast x integreerimist sulgudesse x asemel. Seejärel korrati seda y ning saadi samuti 1/2, mis andis eelneva vastusega kokku 1. Pärast z leidmist lisati veel üks 1/2 juurde saades koguvastuseks 3/2.

Pinnaintegraalid on topeltintegraalid mingist piiratud pinnast. Kui pind on skalaarväli ehk igas selles punktis on arvuline väärtus, siis leiab integraaliga mingi arvulise väärtuse kuid kui pind on vektorväli, kus igas punktis on eraldi vektor, siis tuleb vastuseks samuti vektor.

Ülemine valem tähistab pinda S, kus iga punkt omab arvulist väärtust. Iga x väärtus kohas f(x) võib kirjeldada tihedust selles punktis ning integraal kogu pinnast võib anda selle kogumassi iga S paksuse kihi kohta. Väärtused s ja t võivad muutuda erinevates S osades. Vertikaalsulgudes leitakse vektori pikkus ja siin leiti x osatuletis s ja t suhtes ning leiti nende ristkorrutis. Ristkorrutises korrutatakse 2 vektori pikkused ja tulemus korrutatakse nendevahelise nurga siinusega.  

Üldine pindala valemi näide kuidas võib edasine arvutuskäik välja paista. Ristkorrutise leidmisel kehtib valem kui pind asub 3D ruumis. Kui valem oli näiteks r=(x,y), siis tuletamisel x suhtes saab x üheks ning y asemel tekib 0. Y suhtes tuletamisel saab x'st 0 ja y'st 1.

Kui on vektorväli v pinnas S, kus igas punktis x asub vektor v(x), siis on valem ise enamjaolt sarnane kuigi see ei leia pindala vaid pigem läbivoolu.

Vektor võib tähistada pinnapunkti elektrivälja, gravitatsiooni või läbivoolu punktis x. Integraaliga võib leida voolu läbi pinna S ajaühiku kohta. Kui vektorid on pinnaga paralleelselt, siis puuduks läbivool, sest vool toimuks pinnaga paralleelselt.

Vektorväljas on vaja leida skalaarkorrutis ja vektorkorrutis. Skalaarkorrutis leitakse igas pinna punktis pinnaga ristuva vektori suhtes. Ristkorrutisega leiab selle pinnaga ristuva vektori.

Integraalidest

Integraalide arvutamine sarnaneb tuletamise vastandiga ja selle kasutusalad on sarnased. Kui tuletamisega sai läbitud teepikkuse järgi leida keskmise kiiruse ja edasi kiirenduse, siis integraalides saab kiirendusest leida kiiruse ja edasi läbitud teepikkuse või anda vähemalt aimduse milline peaks rohkemate muutujatega valem umbes välja nägema.
Mõned näited integreerimisreeglitest:

C tähistab mingit arvulist suurust, mis lisatakse integreerimisel. Kui integraalimärgi järel oli x mingis astmes, siis pärast integreerimist liidetakse astmele 1 ja astmesse pandud arv jagatakse uue astme väärtusega.

Lihtsalt arvu integreerimisel korrutatakse see uue väärtusega ja liidetakse C.
Need kaks näidet kirjeldavad teise pildi loogikat. Alustades kiirendusega a sai sellest pärast integreerimist at (aeg lisati uue väärtusena)+ C rollis v0, mis kirjeldas algkiirust. Sellisena oleks vastus potentsiaalselt nullist erinev isegi kui kiirendus oli 0, sest liidetud algkiiruse väärtus võis olla nullist erinev. Asukoha leidmise valemis suurendati kiiruse valemis olnud suuruseid t'ga korrutades (eelmisest valemist võetud algkiirus korrutati t'ga) ning saadi valem, mis arvestab korraga kiirenduse, kiiruse ja stardikohaga y0. Kiirendus korda aeg ruudus jagatud 2 üksi tähistab läbitud teepikkust kui alustada paigalseisust.

Teine võimalus esimese pildi seoste tähistamiseks.
Mõned teised näited tuletamise reeglitest:

 

 

 

Viimases näites tähistavad a ja b integraalimärgi otste juures integraali algus ja lõpppunkti. Suur F tähistab integraali leidmisel saadud tehet ning lahutamisega leitakse nende erinevused kui saadud valemis leida integraal b ja a väärtusega. Kui algkoht on 0, siis on tihti F(0) väärtus samuti 0 ja seda ei tähistata tihti valemi pikemas lahenduskäigus.

Pindala leidmises:

 

Kui graafiku y väärtus on sirge, siis saab selle pindala leida põhikoolist tuttava kõrguse ja laiuse korrutamisega ning kolmnurga puhul ristküliku valemi kahega jagamisega kuigi seda saaks veel integraalidega leida.

 

 Keerulisema pindala leidmine:

Graafiku kõrguse valemis leitakse integraal ning kuna F(0) annab siin -(0+C), siis puudub C rollis väärtus F(2) arvutamisel.

Elektrivoo kirjeldamises saab kasutada integraale. Ülal illustratsioonil on A pisikese pinnaosaga ristisuunas ja E tähistab elektrivälja suunda. Nende vahelisest nurgast võetakse koosinus ja sellest tulemus korrutatakse A ja E väärtusega. Voog on suhteliselt suurem kui E ja A on samasuunalised ja seda väiksemad mida suurema nurga all elektriväli pinda läbib. Integraalita voo valemis tuleb leida laenguga osakeste arv Q ja jagada see vaakumi elektrilise läbitavusega. Integraalis liidetakse kokku iga pisikest ala dA läbivad elektrivälja vood.